Moment of Inertia

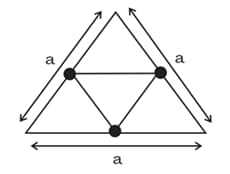
From a triangular lamina of side a and mass $m$ , a small triangular Lamina made by joining mid-points of sides of triangular lamina is cut. If Moment of Inertia of complete Lamina about COM is $I_o$ and Moment of Inertia of remaining Lamina about centroid is $\frac{x{I}_0}{16}$, then find the value of $x$.

Four point masses $($each of mass $m$$)$ are arranged in the $X-Y$ plane. The moment of inertia of this array of masses about $Y$-axis is 

M.O.I is the ratio of 

A solid sphere, a thin ring and a cylinder of same mass and radius, held at rest are released simultaneously to roll down on an inclined plane. Which one will reach the bottom first?

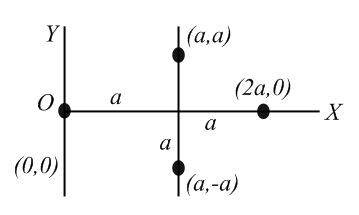
Point masses $1, 2, 3$ and $4 \mathrm{kg}$ are lying at the points $(0, 0, 0), (2, 0, 0), (0, 3, 0)$ and $(-2, -2, 0)$, respectively. The moment of inertia of this system about the $x$-axis will be,

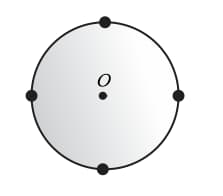
Four similar point masses (each of mass $m$) are placed on the circumference of a disk of mass $M$ and radius $R$. The moment of inertia of the system about the normal axis through the center $O$ will be,

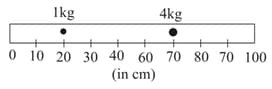
On the marks of $20 \mathrm{cm}$ and $70 \mathrm{cm}$ of a light meter scale, two weights, $1 \mathrm{kg}$ and $4 \mathrm{kg}$, respectively, are placed. The moment of inertia (in $\mathrm{kg} {\mathrm{m}}^2$) about the vertical axis through the $100 \mathrm{cm}$ mark will be,

M.O.I is the ratio of 

M.O.I. of a disc is minimum about an axis 

The moment of inertia of hollow cylinder having density $\rho$ and height $h$ is $\frac{\pi \rho h{r}^4}{2}$.

Describe the term moment of inertia of hollow cylinder?

The moment of inertia of a hollow cylinder of mass $M$ and inner radius $R_1$ and outer radius $R_2$ about its central axis is

A flywheel is used in an automobile engine due to its:

Why fly wheels are used in vehicles?

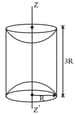
A solid cylinder is made of radius R and height 3R having mass density $\rho$ . Now two half spheres of radius R are removed from both ends. The moment of inertia of remaining portion about axis ZZ' can be calculated as $\frac{29}{6K}\pi R^5\rho$ . Find K.

A uniform thin bar of mass $6 \mathrm{kg}$ and length $2.4$ meter is bent to make an equilateral hexagon. The moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of hexagon is ________ $\times {10}^{-1} \mathrm{kg} {\mathrm{m}}^2$

These questions consists of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: If we draw a circle around the centre of mass of a rigid body, then moment of inertia about all parallel axes passing through this circle has a constant value.
Reason: Dimensions of radius of gyration are $\left[{\mathrm{M}}^0{\mathrm{LT}}^0\right]$

A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular, its moment of inertia

The inductance in a coil plays the same role as

The moment of inertia of a rigid body depends on: